图像内容和风格都是比较抽象的,这篇文章通过深度学习,提取了图像内容和风格,并将两者合并,生成新的图像。
A Neural Algorithm of Artistic Style
标签(空格分隔): PaperRead
画家画画有独特的风格。之前,没有人工智能系统可以学习画的风格。深度学习在图像分类、人脸识别、物体检测等领域取得了成功。本文提出基于深度学习的算法,将画的内容(content)和风格(style)区分开来。取一幅画的style,另一幅画的content,将两者合并创造出新的画。
卷积神经网络通过不同的Layer学习不同feature,每层的输出都是一系列的feature map。
当训练神经网络进行object recognition时,不同的层学习到图像的不同表示。从输入的像素值逐渐到图像内容。通过不同层的feature map重建,可以看出,higher layer学习到的是high-level content;lower layer的feature map重建是提取了原图的像素值。
通过设计捕捉纹理信息(texture information)的feature空间,来得到图像style的表示。feature空间基于top filter response,包含了不同空间的filter response的相关性。最终得到了图像不同尺度的捕捉texture information的表示。
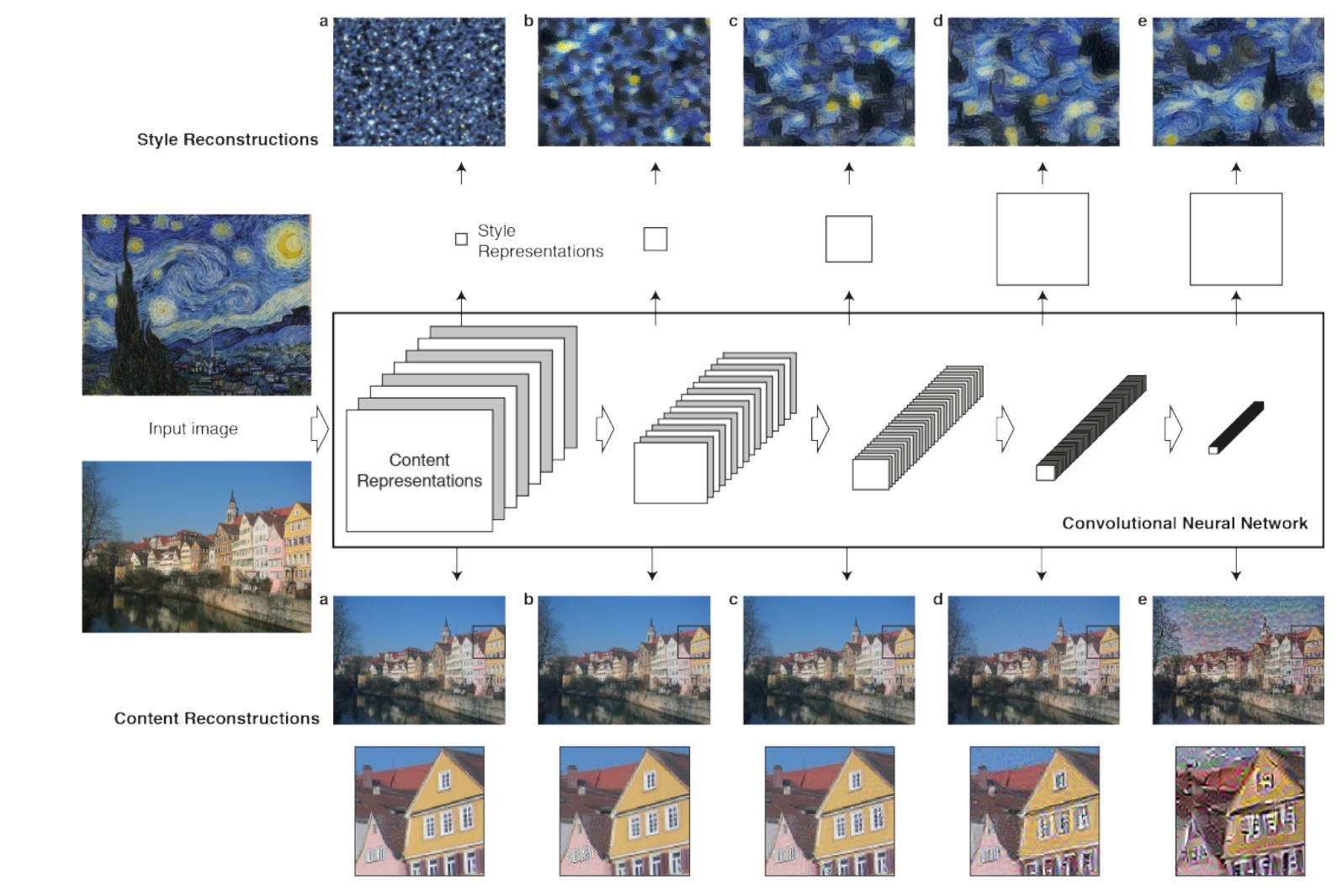
上图表示给定输入图像,不同层的feature map的表示。网络越深,filter越多,但是filtered image size在减小。
Content ReConstruction,通过VGG-Network的‘conv1_1(a)’, ‘conv2_1(b)’, ‘conv3_1(d)’, ‘conv5_1(e)’的feature map重建输入图像。lower layer(a,b,c)重建的图像很接近原图,higher layer重建得到图像content。
Style Reconstruction, 在原始CNN表示的顶端构建了新的feature空间来捕获输入图像的style。style表示计算不同layer feature的相关性。在layer的子集上重建( ‘conv1 1’ (a), ‘conv1 1’ and ‘conv2 1’ (b), ‘conv1 1’, ‘conv2 1’ and ‘conv3 1’ (c), ‘conv1 1’, ‘conv2 1’, ‘conv3 1’ and ‘conv4 1’ (d), ‘conv1 1’, ‘conv2 1’, ‘conv3 1’, ‘conv4 1’
and ‘conv5 1’ (e))。丢弃scene信息越多,越能得到图像的style。从style feature生成关于图像的纹理,就是呈现出颜色和局部结构。
这篇文章主要发现就是通过卷积神经网络可以将图像的content和style分开。这样可以将不同图像的content和style合成,生成新的图像。将图像内容和名画style合成,如下图所示:
通过不同层来生成style,可以得到不同合成图片(下图行之间的对比)。通过higher layer来生成时,生成图像效果更好(下图最后一行)。
style和content不存在完美的合成。在合成时,最小化的loss函数包含content loss和style loss。权重不同,生成图片不同(如下图列之间对比)。

上图每列上面的数字是$\alpha / \beta$的比值,即content和style重要性。
Methods
这里使用VGG-Network,具体是16个卷积层和5个pooling层的19层网络。没有使用全连接层。将max-pooling替换为average pooling,改善梯度流动,可以得到更好结果。
一个layer,有$N_l$个不同的filter,包含$N_l$个feature map,feature map大小为width x height = $M_l$。layer $l$的相应可以存储到矩阵$F^l \in R^{N_l \times Ml}$,$F{ij}^l$表示$l$层的第$i$个fiter在$j$位置的激活值。为了根据content生存图像,用白噪声图像$\vec x$和原图$\vec p$输入到网络,得到不同层的激活值$P^l$和$F^l$,最小化它们之间的平方差,使用它梯度下降法得到$\vec p$
$$ L_{content}(\vec p, \vec x, l) = \frac{1}{2} \sum_{ij}(F_{ij}^l - P_{ij}^l) $$损失函数对第$l$层的激活值求导:
$$ \frac{\partial L_{content}}{\partial F_{ij}^l} = \left\{ \begin{array}{rl} (F^l - P^l)_{ij} \quad if \quad F_{ij}^l > 0\\ 0 \qquad \qquad \quad if \quad F_{ij}^l < 0 \end{array} \right. $$使用反向传播,训练,改变白噪声图像$\vec x$的值,这样得到的图像content会和原图$\vec p$content相近。重建content使用的是VGG的五个层。
重建content,是根据激活值来重建。重建style,是根据不同filter得到的激活值之间的相关性来重建。因为style在图像中的表现就是纹理特征,即像素之间的相关性。到了high-lever layer,体现在不同feature map之间的相关性上。通过求得Gram矩阵$G^l \in R^{N_l \times Nl}$,这里的$G{ij}^l$是第$l$层$i$和$j$ feature map向量化后的内积
$$ G_{ij}^l = \sum_k F_{ik}^l F_{jk}^l $$原图像$\vec a$和白噪声图像$\vec x$,分别计算$l$层的Gram矩阵$A^l$和$G^l$,这一层的loss函数为:
$$ E_l = \frac{1}{4N_l^2 M_l^2} \sum_{ij}(G_{ij}^l - A_{ij}^l)^2 $$总的loss
$$ L_{style}(\vec a, \vec x) = \sum_{l=0}^L w_l E_l $$$w_l$表示第$l$层的权重。$E_l$关于$l$层激活值的导数:
$$ \frac{\partial E_l}{\partial F_{ij}^l} = \left\{ \begin{array}{rl} \frac{1}{N_l^2 M_l^2} ((F^l)^T (G^l - A^l))_{ji}\quad if \quad F_{ij}^l > 0\\ 0 \qquad \qquad \qquad \qquad \qquad \qquad if \quad F_{ij}^l < 0 \end{array} \right. $$求得总的loss,$\vec p$是content原图,$\vec a$是style原图。
$$ L_{total}(\vec p, \vec a, \vec x) = \alpha L_{contenx}(\vec p, \vec x) + \beta L_{style}(\vec a, \vec x) $$$\alpha$和$\beta$关于content和style的权重系数,$\alpha / \beta$比值,决定生成的图像更多来自style还是content。前面图片有展示。